PROGRAMACIÓN DEL TEMA DE LAS FRACCIONES EN 1º DE ESO
Sesiones | Metodología |
1ª / | - Explicar concepto de fracción, los 3 significados de una fracción. - Fracción propia e impropia. - Signo de una fracción. Representación gráfica de las fracciones. - Ejercicios pág. 69 (1 a 5 y 7 a 9). |
2ª / | - Corregir sesión anterior. - Fracciones equivalentes, cómo saber si dos fracciones son equivalentes, obtención de frac. equivalentes (Propiedad fundamental de las fracciones), simplificar fracciones. - Ejercicios pág. 71 (10 a 12 y 15 a 16). |
3ª / | - Corregir sesión anterior. - Recordar procedimiento cálculo mcm. - Explicar reducción frac. a común denominador. - Ejercicios pág. 71 (13 y 14) y 76 (45). |
4ª / | - Corregir sesión anterior. - Explicar suma y resta de fracciones. - Ejerc. pág. 73 (17 a 24). |
5ª / | - Corregir sesión anterior. - Explicar producto de fracciones. - Ejerc. pág. 75 (25), 77 (55, 56, 66 y 68), 78 (82 a 84). |
6ª / | - Corregir sesión anterior. - Explicar división de fracciones. - Ejerc. pág. 75 (26 a 30), 77 (57 a 60). |
7ª / | - Corregir ejercicios de la sesión anterior. - Problemas. Ejercicios pág. 80 (105 a 107 y 110 a 113) |
8ª / | - Corregir ejercicios de la sesión anterior. - Estudiar |
9ª / | - CONTROL. |
DESARROLLO DEL TEMA
TEMA 4: LAS FRACCIONES
Una fracción consta de dos números enteros dispuestos de esta forma: 
a es el numerador e indica las partes que se toman.
b es el denominador e indica las partes en que se divide la unidad (b ≠ 0).
Así, por ejemplo, en la fracción 
a) Como una parte de la unidad: Se divide a la unidad en tantas partes iguales como indica el denominador y se toman las partes que indique el numerador.
b) Como una división: El numerador es el dividendo y el denominador es el divisor.
c) Como un operador: Cuando hay que hallar la fracción de un número, se multiplica la fracción por el número (se multiplica el numerador por el número y se divide el resultado entre el denominador).
Clases de fracciones:
a) PROPIA: Si el numerador es menor que el denominador:
b) IMPROPIA: Si el numerador es mayor que el denominador:
c) UNIDAD: Si el numerador es igual que el denominador: 
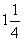
Signo de una fracción: Como la fracción es una división,
a) Si los dos términos tienen el mismo signo, el resultado es positivo.
b) Si tienen distinto signo, el resultado es negativo.
Si una fracción es negativa, el signo menos se escribe delante de la fracción y nunca en el numerador ni mucho menos en el denominador.
Fracciones equivalentes:
Son las que tienen el mismo valor.
Cómo saber si dos fracciones son equivalentes:
a) Si al dividir el numerador entre el denominador el resultado es igual en ambas fracciones.
b) Comparando si son iguales los productos cruzados.
Cómo obtener fracciones equivalentes.
a) Por amplificación: Multiplicando a los dos términos de la fracción por un mismo número.
b) Por simplificación: Dividiendo, si se puede, a los dos términos de la fracción por un mismo número.
Si una fracción no se puede simplificar se llama IRREDUCIBLE.
[Propiedad fundamental: si a los dos términos de una fracción se les multiplica o divide por un mismo número resulta una fracción equivalente].
Reducir fracciones a común denominador: Se trata de obtener fracciones equivalentes a las primeras, cuyos denominadores sean el mínimo común múltiplo de los denominadores y los numeradores se obtengan dividiendo el denominador común entre cada denominador y multiplicando el resultado por el numerador correspondiente.
La reducción de fracciones a común denominador se utiliza para comparar fracciones y para sumarlas y restarlas.
a) Fracciones con el mismo denominador: Es mayor la que tenga mayor numerador.
b) Fracciones con el mismo numerador: Es mayor la que tenga menor denominador.
Sumar y restar fracciones:
Para sumar o restar fracciones se reducen a común denominador, hallando el mcm de los denominadores, dividiendo éste (el mcm) entre los denominadores iniciales y multiplicando cada cociente por el correspondiente numerador. El resultado es una fracción cuyo numerador es la suma o resta de los numeradores obtenidos y cuyo denominador es el mcm de los denominadores.
El resultado final siempre se simplifica, si se puede dividir al numerador y al denominador por un mismo número hasta obtener la fracción irreducible.
Si hay que sumar o restar una fracción con un entero, se considera al entero como una fracción con denominador 1.
Es otra fracción cuyo numerador es el producto de los numeradores y cuyo denominador es el producto de los denominadores.
División de fracciones:
Para dividir fracciones se multiplica la primera (dividendo) por la inversa de la segunda (divisor).
El resultado final siempre se simplifica si se puede dividir al numerador y al denominador por un mismo número.
